Simpson's Rule and procedures

Simpson's Rule

by M. Bourne

Interactive exploration

See an applet where you can explore Simpson's Rule and other numerical techniques:
Riemann Sums Applet

In the last section, Trapezoidal Rule, we used straight lines to model a curve and learned that it was an improvement over using rectangles for finding areas under curves because we had much less "missing" from each segment.

We seek an even better approximation for the area under a curve.

In Simpson's Rule, we will use parabolas to approximate each part of the curve. This proves to be very efficient since it's generally more accurate than the other numerical methods we've seen. (See more about Parabolas.)

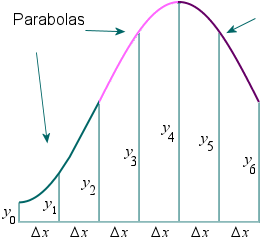
We divide the area into $\displaystyle{n}$ equal segments of width $\displaystyle\Delta{x}$. The approximate area is given by the following.

Simpson's Rule

Area $\displaystyle={\int_{{a}}^{{b}}} f{{\left({x}\right)}}{\left.{d}{x}\right.}$

$\displaystyle\approx\frac{{\Delta{x}}}{{3}}{\left({y}_{{0}}+{4}{y}_{{1}}+{2}{y}_{{2}}+{4}{y}_{{3}}+{2}{y}_{{4}}+\right.}$ $\displaystyle{\left.\ldots+{4}{y}_{{{n}-{1}}}+{y}_{{n}}\right)}$

where $\displaystyle\Delta{x}=\frac{{{b}-{a}}}{{n}}$

Note: In Simpson's Rule, n must be EVEN.

See below how we obtain Simpson's Rule by finding the area under each parabola and adding the areas.

Memory aid

We can re-write Simpson's Rule by grouping it as follows:

$\displaystyle{\int_{{a}}^{{b}}} f{{\left({x}\right)}}{\left.{d}{x}\right.}$ $\displaystyle\approx\frac{{\Delta{x}}}{{3}}{\left[{y}_{{0}}+{4}{\left({y}_{{1}}+{y}_{{3}}+{y}_{{5}}+\ldots\right)}\right.}$ $\displaystyle{\left.+{2}{\left({y}_{{2}}+{y}_{{4}}+{y}_{{6}}+\ldots\right)}+{y}_{{n}}\right]}$

This gives us an easy way to remember Simpson's Rule:

$\displaystyle{\int_{{a}}^{{b}}} f{{\left({x}\right)}}{\left.{d}{x}\right.}$ $\displaystyle\approx\frac{{\Delta{x}}}{{3}}{\left[\text{FIRST}+{4}{\left(\text{sum of ODDs}\right)}\right.}$ $\displaystyle{\left.+{2}{\left(\text{sum of EVENs}\right)}+\text{LAST}\right]}$

Example using Simpson's Rule

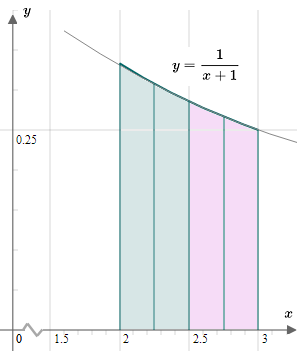
Approximate $\displaystyle{\int_{{2}}^{{3}}}\frac{{{\left.{d}{x}\right.}}}{{{x}+{1}}}$ using Simpson's Rule with $\displaystyle{n}={4}$.

We haven't seen how to integrate this using algebraic processes yet, but we can use Simpson's Rule to get a good approximation for the value.

Here is the situation.

$\displaystyle\Delta{x}=\frac{{{b}-{a}}}{{n}}=\frac{{{3}-{2}}}{{4}}={0.25}$

$\displaystyle{y}_{{0}}= f{{\left({a}\right)}}$

$\displaystyle= f{{\left({2}\right)}}$

$\displaystyle=\frac{1}{{{2}+{1}}}={0.3333333}$

$\displaystyle{y}_{{1}}= f{{\left({a}+\Delta{x}\right)}}= f{{\left({2.25}\right)}}$ $\displaystyle=\frac{1}{{{2.25}+{1}}}={0.3076923}$

$\displaystyle{y}_{{2}}= f{{\left({a}+{2}\Delta{x}\right)}}= f{{\left({2.5}\right)}}$ $\displaystyle=\frac{1}{{{2.5}+{1}}}={0.2857142}$

$\displaystyle{y}_{{3}}= f{{\left({a}+{3}\Delta{x}\right)}}= f{{\left({2.75}\right)}}$ $\displaystyle=\frac{1}{{{2.75}+{1}}}={0.2666667}$

$\displaystyle{y}_{{4}}= f{{\left({b}\right)}}= f{{\left({3}\right)}}$ $\displaystyle=\frac{1}{{{3}+{1}}}={0.25}$

So

Area $\displaystyle={\int_{{a}}^{{b}}} f{{\left({x}\right)}}\text{d}{x}$

$\displaystyle\approx\frac{0.25}{{3}}{\left({0.333333}+{4}{\left({0.3076923}\right)}\right.}$ $\displaystyle+{2}{\left({0.2857142}\right)}+{4}{\left({0.2666667}\right)}$ $\displaystyle{\left.+{0.25}\right)}$

$\displaystyle={0.2876831}$

Notes

1. The actual answer to this problem is 0.287682 (to 6 decimal places) so our Simpson's Rule approximation has an error of only 0.00036%.

2. In this example, the curve is very nearly parabolic, so the 2 parabolas shown above practically merge with the curve $\displaystyle{y}=\frac{1}{{{x}+{1}}}$.

GIS Blog (It's All About GIS): ET SpatialTechniques Products v11.3 for ArcGIS 10....

GIS Blog (It's All About GIS): ET SpatialTechniques Products v11.3 for ArcGIS 10....: ET GeoTools is a set of tools for ArcGIS which purpose is to increase the editing productivity in ArcMap, give enhanced editing functiona...

GIS Blog (It's All About GIS): Blue Marble Global Mapper 18 Full Crack Download

GIS Blog (It's All About GIS): Blue Marble Global Mapper 18 Full Crack Download: Global Mapper Overview Equally well suited as a standalone spatial data management tool and as an integral component of an enterprise-wi...

GIS Blog (It's All About GIS): OkMap v13.4.1 Full Crack Download

GIS Blog (It's All About GIS): OkMap v13.4.1 Full Crack Download: OkMap is an interactive software which allows you to work on your computer screen with web maps or digital maps that you have either bough...

GIS Blog (It's All About GIS): Bentley Acute3D ContextCapture Center v4 Full Crac...

GIS Blog (It's All About GIS): Bentley Acute3D ContextCapture Center v4 Full Crac...: Acute3D, a Bentley Systems company, develops and sells ContextCapture, a new solution developed on the basis of the former Smart3DCapture...

GIS Blog (It's All About GIS): ERDAS IMAGINE 9 FULL CRACK DOWNLOAD WITH LPS

GIS Blog (It's All About GIS): ERDAS IMAGINE 9 FULL CRACK DOWNLOAD WITH LPS: ERDAS IMAGINE is a powerful remote sensing and image analysis program. It is a gateway to multiple integrated geospatial technologies, int...

GIS Blog (It's All About GIS): Rockware Rockworks Full Crack Download

GIS Blog (It's All About GIS): Rockware Rockworks Full Crack Download: RockWorks is the standard in the petroleum, environmental, geotechnical and mining industries for surface and subsurface data visuali...