Traverse Correction - Bowditch Method

In Traversing the lengths of the line are measured by chain or a tape and the directions are fixed by the compass or theodolite or by forming angles with chain and a tape. The latest instruments like total station captures the co-ordinates of the points along with elevations. These instruments are also capable of recording and string the distances and angles replacing the conventional methods.

There are two types of traverse surveying i.e. Closed Traverse and Open Traverse.

1. Closed Traverse: 
   When a series of connected lines form a closed circuit, ie. When the finishing point coincides with the starting point, then it is called as a closed traverse. These closed traverse surveys has many applications like fixing the boundaries of ponds, forests etc..

2. Open traverse :
   When a sequence of connected lines extends along a general direction and does not return to the starting point, it is known as ‘open traverse’ or ‘unclosed traverse’.

Traverse Correction Procedure

Present techniques used in traversing using total station as a open traverse. The steps are as described below…

1. GPS pair points are fixed at a convenient distance, approximately about 3 to 5km. Care has to be taken that the pair of GPS points is fixed at a reliable distance (at least 60m is advised for better results) and on good monuments. These points are fixed in such a way that they are clearly inter visible and should cater for placing the total station firmly on the GPS stations,
2. Total station is to be checked for its calibration, prism constants for the prisms to be set in the instrument to avoid errors.
3. Total station is then used to conduct the traverse between the GPS points. This type of traverse ensures that the survey is started from a known pair of points and is closed on known pair of points. Care has to be taken that the last bearing is also taken for correcting the misclosures.
4. There are several methods to correct the traverse misclosures. However, in most of the cases Bowditch rule is considered to be most reliable. The other methods like transit method, Crandall method, Least Square Methods are used very rarely. The most accurate method which is known as a misclosures correction by the least square method is used when the accuracy required is very high. This method finds itself applicable in the projects like tunnel works.

1. Bowditch Rule
2. Whole Circle Bearing
3. Quandrantal Bearing

TOTAL STATION TRAVERSING ADJUSTMENT BY BOWDITCH METHOD

TOTAL STATION TRAVERSING ADJUSTMENT BY BOWDITCH METHOD

PROCEDURE FOR TRAVERSE CALCULATIONS

• Adjust angles or directions
• Determine bearings or azimuths
• Calculate and adjust latitudes and departures
• Calculate rectangular coordinates

DETERMINING BEARINGS OR AZIMUTHS

• Requires the direction of at least one line within the traverse to be known or assumed
• For many purposes, an assumed direction is sufficient
• A magnetic bearing of one of the lines may be measured and used as the reference for determining the other directions
• For boundary surveys, true directions are needed

LATITUDES AND DEPARTURES

Line	Dir	Deg	Min	Sec	Dir	Degrees	Length	Cumulative Length	Azimuthal Angles	Departure	Latitude
AB	N	26	10	0	E	N26.167E	285.1	285.1	26.167	+125.726	+255.881
BC	S	75	25	0	E	S75.417E	610.45	895.55	+104.583	+590.784	-153.700
CD	S	15	30	0	W	S15.5W	720.48	1616.03	+195.500	-192.540	-694.276
DE	N	1	42	0	W	N1.7W	203	1819.03	+358.300	-6.022	+202.911
EA	N	53	0	0	W	N53W	647.02	2466.05	+307.000	-516.733	+389.386

CLOSURE OF LATITUDES AND DEPARTURES

• The algebraic sum of all latitudes must equal zero or the difference in latitude between the initial and final control points
• The algebraic sum of all departures must equal zero or the difference in departure between the initial and final control points

ADJUSTMENT OF LATITUDES AND DEPARTURES

Line	Dir	Deg	Min	Sec	Dir	Length	Cumulative Length	Azimuthal Angles	Departure	Latitude
AB	N	26	10	0	E	285.1	285.1	26.167	+125.726	+255.881
BC	S	75	25	0	E	610.45	895.55	+104.583	+590.784	-153.700
CD	S	15	30	0	W	720.48	1616.03	+195.500	-192.540	-694.276
DE	N	1	42	0	W	203	1819.03	+358.300	-6.022	+202.911
EA	N	53	0	0	W	647.02	2466.05	+307.000	-516.733	+389.386

 

ADJUSTED LATITUDES AND DEPARTURES

Line

Dir

Deg

Min

Sec

Dir

Length

Cumulative Length

Azimuthal Angles

Departure Misclosure

Latitude Misclosue

Corrected Departure

Corrected Latitude

AB

N

26

10

0

E

285.1

285.1

26.167

+0.140

+0.023

+125.586

+255.858

BC

S

75

25

0

E

610.45

895.55

+104.583

+0.301

+0.050

+590.483

-153.750

CD

S

15

30

0

W

720.48

1616.03

+195.500

+0.355

+0.059

-192.895

-694.335

DE

N

1

42

0

W

203

1819.03

+358.300

+0.100

+0.017

-6.122

+202.894

EA

N

53

0

0

W

647.02

2466.05

+307.000

+0.319

+0.053

-517.052

+389.334

                                                                                                                                                αCorr.Dep=0      αCorr.Lat=0

The Sum of total Corrected Departure and Sum of total Corrected latitude is 0.00, proves that the traverse is balanced

RECTANGULAR COORDINATES

• Rectangular X and Y coordinates of any point give its position with respect to a reference coordinate system
• Useful for determining length and direction of lines, calculating areas, and locating points
• You need one starting point on a traverse (which may be arbitrarily defined) to calculate the coordinates of all other points
• A large initial coordinate is often chosen to avoid negative values, making calculations easier.

CALCULATING X AND Y COORDINATES

Given the X and Y coordinates of any starting point A, the X and Y coordinates of the next point B are determined by:

Line	Dir	Deg	Min	Sec	Dir	Length	Azimuthal Angles	Calculated Easting	Calculated Northing	Adjusted Easting	Corrected Northing
AB	N	26	10	0	E	285.1	26.167	+5125.726	+10255.881	+5125.586	+10255.858
BC	S	75	25	0	E	610.45	+104.583	+5716.510	+10102.180	+5716.069	+10102.107
CD	S	15	30	0	W	720.48	+195.500	+5523.970	+9407.904	+5523.174	+9407.772
DE	N	1	42	0	W	203	+358.300	+5517.948	+9610.815	+5517.052	+9610.666
EA	N	53	0	0	W	647.02	+307.000	+5001.214	+10000.201	+5000.000	+10000.000

LINEAR MISCLOSURE

The hypotenuse of a right triangle whose sides are the misclosure in latitude and the misclosure in departure.

TRAVERSE PRECISION

• The precision of a traverse is expressed as the ratio of linear misclosure divided by the traverse perimeter length.
• expressed in reciprocal form
• Example

0.89 / 2466.05 = 0.00036090
1 / 0.00036090 = 2770.8

Precision = 1/2771

Lesson Note on methods used to determine azimuth by observations of the sun.

At what time will the effects of a small error in the determination of observer's latitude be minimized when making azimuth observations on Polaris?
A. 12:00 midnight
B. when Polaris is at elongation
C. when Polaris is at culmination
D. when the LHA is 90 degrees
E. when the GHA is 90 degrees
Ans; C. At culmination the bearing is 0 at all LAT.

There are two methods by which azimuth can be determined by observation of the sun. Answer the following questions concerning these methods.


QS > Name the two methods that can be used to determine azimuth by observations of the sun.
Ana; 1. Altitude method and
           2. hour angle method.

QS>Which method is more accurate? Explain your answer.
Ans; Hour angle method—because time can be very accurately determined, and inaccuracies in measuring the vertical angle and determining refraction make the altitude method less reliable.

Lesson Note On Solving plane triangles

Solving plane trianglesEdit

Standard notation for a triangle

A general form triangle has six main characteristics (see picture): three linear (side lengths a, b, c) and three angular (α, β, γ). The classical plane trigonometry problem is to specify three of the six characteristics and determine the other three. A triangle can be uniquely determined in this sense when given any of the following:

• Three sides (SSS)
• Two sides and the included angle (SAS)
• Two sides and an angle not included between them (SSA), if the side length adjacent to the angle is shorter than the other side length.
• A side and the two angles adjacent to it (ASA)
• A side, the angle opposite to it and an angle adjacent to it (AAS).
• Three angles (AAA) on the sphere (but not in the plane).

For all cases in the plane, at least one of the side lengths must be specified.

 If only the angles are given, the side lengths cannot be determined, because any similar triangle is a solution

Trigonomic relations

The standard method of solving the problem is to use fundamental relations.

Law of cosines

${\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha }$

${\displaystyle b^{2}=a^{2}+c^{2}-2ac\cos \beta }$

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma }$

Law of sines

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}}$

Sum of angles

${\displaystyle \alpha +\beta +\gamma =180^{\circ }}$

Law of tangents

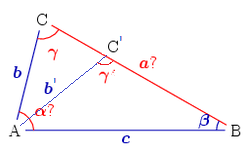
${\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.}$

There are other (sometimes practically useful) universal relations:

 the law of cotangents and Mollweide's formula.

NotesEdit

1. To find an unknown angle, the law of cosines is safer than the law of sines. The reason is that the value of sine for the angle of the triangle does not uniquely determine this angle. For example, if sin β = 0.5, the angle β can equal either 30° or 150°. Using the law of cosines avoids this problem: within the interval from 0° to 180° the cosine value unambiguously determines its angle. On the other hand, if the angle is small (or close to 180°), then it is more robust numerically to determine it from its sine than its cosine because the arc-cosine function has a divergent derivative at 1 (or −1).
2. We assume that the relative position of specified characteristics is known. If not, the mirror reflection of the triangle will also be a solution. For example, three side lengths uniquely define either a triangle or its reflection.

Three sides given (SSS)Edit

Three sides given

Let three side lengths a, b, c be specified. To find the angles α, β, the law of cosines can be used:

${\displaystyle {\begin{aligned}\alpha &=\arccos {\frac {b^{2}+c^{2}-a^{2}}{2bc}}\\[4pt]\beta &=\arccos {\frac {a^{2}+c^{2}-b^{2}}{2ac}}.\end{aligned}}}$

Then angle γ = 180° − α − β.

Some sources recommend to find angle β from the law of sines but (as Note 1 above states) there is a risk of confusing an acute angle value with an obtuse one.

Another method of calculating the angles from known sides is to apply the law of cotangents.

Two sides and the included angle given (SAS)Edit

Two sides and the included angle given

Here the lengths of sides a, b and the angle γ between these sides are known. The third side can be determined from the law of cosines:

${\displaystyle c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}.}$

Now we use law of cosines to find the second angle:

${\displaystyle \alpha =\arccos {\frac {b^{2}+c^{2}-a^{2}}{2bc}}.}$

Finally, β = 180° − α − γ.

Two sides and non-included angle given (SSA)Edit

Two sides and a non-included angle given

Two solutions for the triangle

This case is not solvable in all cases; a solution is guaranteed to be unique only if the side length adjacent to the angle is shorter than the other side length. Assume that two sides b, c and the angle β are known. The equation for the angle γ can be implied from the law of sines:

${\displaystyle \sin \gamma ={\frac {c}{b}}\sin \beta .}$

We denote further D = c/b sin β (the equation's right side). There are four possible cases:

1. If D > 1, no such triangle exists because the side b does not reach line BC. For the same reason a solution does not exist if the angle β ≥ 90° and b ≤ c.
2. If D = 1, a unique solution exists: γ = 90°, i.e., the triangle is right-angled.
3. If D < 1 two alternatives are possible.
   1. If b ≥ c, then β ≥ γ (the larger side corresponds to a larger angle). Since no triangle can have two obtuse angles, γ is an acute angle and the solution γ = arcsin D is unique.
   2. If b < c, the angle γ may be acute: γ = arcsin D or obtuse: γ′ = 180° - γ. The figure on right shows the point C, the side b and the angle γ as the first solution, and the point C′, side b′ and the angle γ′ as the second solution.

Once γ is obtained, the third angle α = 180° − β − γ.

The third side can then be found from the law of sines:

${\displaystyle a=b\ {\frac {\sin \alpha }{\sin \beta }}}$

or

${\displaystyle a=c\cos \beta \pm {\sqrt {b^{2}-c^{2}\sin ^{2}\beta }}}$

A side and two adjacent angles given (ASA)Edit

One side and two adjacent angles given

The known characteristics are the side c and the angles α, β. The third angle γ = 180° − α − β.

Two unknown side can be calculated from the law of sines:

${\displaystyle a=c\ {\frac {\sin \alpha }{\sin \gamma }};\quad b=c\ {\frac {\sin \beta }{\sin \gamma }}.}$

or

${\displaystyle a=c{\frac {\sin \alpha }{\sin \alpha \cos \beta +\sin \beta \cos \alpha }}}$

${\displaystyle b=c{\frac {\sin \beta }{\sin \alpha \cos \beta +\sin \beta \cos \alpha }}}$