Friday, 9 August 2019
Tech BD: Free Download Adobe Illustrator CC 2016 Full + Cra...
Tech BD: Free Download Adobe Illustrator CC 2016 Full + Cra...: Free Download Adobe Illustrator CC 2016 Full + Crack (32bit, 64bit) Adobe Illustrator is a vector graphics p...
Saturday, 27 July 2019
The Trapezoidal Rule
The Trapezoidal Rule
by M. Bourne
Interactive exploration
See an applet where you can explore Simpson's Rule and other numerical techniques:Riemann Sums Applet
Problem: Find
∫01x2+1 dx
We put u=x2+1 then du=2x dx.
But the question does not contain an `x\ dx` term so we cannot solve it using any of the integration methods we have met so far.
We need to use numerical approaches. (This is usually how software like Mathcad or graphics calculators perform definite integrals).
We can use one of two methods:
- Trapezoidal rule
- Simpson's Rule (in the next section: Simpson's Rule)
Continues below ⇩
The Trapezoidal Rule
We saw the basic idea in our first attempt at solving the area under the arches problem earlier.
Instead of using rectangles as we did in the arches problem, we'll use trapezoids (trapeziums) and we'll find that it gives a better approximation to the area.
y0
Δx
y1
Δx
y2
Δx
y3
Δx
y4
Δx
y5
Δx
y6
The approximate area under the curve is found by adding the area of all the trapezoids.
(Recall that we write "Δx" to mean "a small change in x".)
Area of a trapezoid
p
q
h
Area=2h(p+q)
Now, the area of a trapezoid (trapezium) is given by:
Area=2h(p+q)
We need "right" trapezoids (which means the parallel sides are at right angles to the base), and they are rotated 90° so that their new base is actually h, as follows, and h = Δx.
y0
y1
Δx
A "typical" trapezoid
So the total area is given by:
Area≈21(y0+y1)Δx+ 21(y1+y2)Δx+ 21(y2+y3)Δx+…
We can simplify this to give us the Trapezoidal Rule, for n trapezoids:
Area≈ Δx(2y0+y1+y2+y3+ …+2yn)
To find Δx for the area from x=a to x=b, we use:
Δx=nb−a
and we also need
y0=f(a)
y1=f(a+Δx)
y2=f(a+2Δx)
…
yn=f(b)
Note
- We get a better approximation if we take more trapezoids [up to a limit!].
- The more trapezoids we take, Δx will tend to 0, that is, Δx→0.
- We can write (if the curve is above the x-axis only between x=a and x=b):
Area=∫abf(x)dx
≈ Δx(2y0+y1+…+2yn)
Don't miss...
There is an interactive applet where you can explore the Trapezoid Rule, here:
Exercise
Using n=5, approximate the integral:
∫01x2+1 dx
Answer
This is the situation:
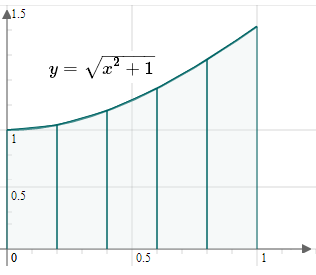
I have joined each of the points at the top of the vertical segments with a straight line.
Here, a=0 and b=1, and the width of each trapezoid is given by:
y1=f(a+Δx)= f(0.2)=0.22+1=1.0198039
y2=f(a+2Δx)= f(0.4)=0.42+1=1.0770330
y3=f(a+3Δx)= f(0.6)=0.62+1=1.1661904
y4=f(a+4Δx)= f(0.8)=0.82+1=1.2806248
y5=f(a+5Δx)= f(1.0)=12+1=1.4142136
So we have:
Integral≈
So ∫01x2+1 dx≈1.150
We can see in the graph above the trapezoids are very close to the original curve, so our approximation should be close to the real value. In fact, to 3 decimal places, the integral value is 1.148.
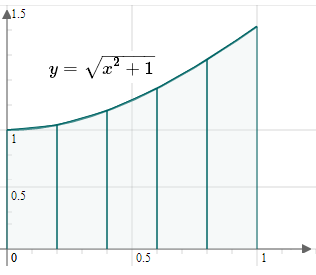
I have joined each of the points at the top of the vertical segments with a straight line.
Here, a=0 and b=1, and the width of each trapezoid is given by:
Δx=nb−a=51−0=0.2y0=f(a)= f(0)=02+1=1
y1=f(a+Δx)= f(0.2)=0.22+1=1.0198039
y2=f(a+2Δx)= f(0.4)=0.42+1=1.0770330
y3=f(a+3Δx)= f(0.6)=0.62+1=1.1661904
y4=f(a+4Δx)= f(0.8)=0.82+1=1.2806248
y5=f(a+5Δx)= f(1.0)=12+1=1.4142136
So we have:
Integral≈
0.2(21×1+1.0198039 +1.0770330+1.1661904 +1.2806248+21×1.4142136)
=1.150So ∫01x2+1 dx≈1.150
We can see in the graph above the trapezoids are very close to the original curve, so our approximation should be close to the real value. In fact, to 3 decimal places, the integral value is 1.148.
Subscribe to:
Comments (Atom)
